Método de Euler
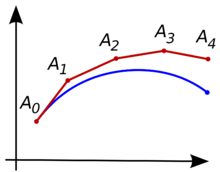
Ilustração do método de Euler. A curva desconhecida está em azul, e sua aproximação polinomial está em vermelho.[1]
Em matemática e ciência computacional, o método de Euler, cujo nome relaciona-se com Leonhard Euler, é um procedimento numérico de primeira ordem para solucionar equações diferenciais ordinárias com um valor inicial dado. É o tipo mais básico de método explícito para integração numérica para equações diferenciais ordinárias.
Índice
1 Formulação do Método de Euler
2 Exemplo
2.1 Usando um passo igual a 1 (h = 1)
2.2 Usando outros tamanhos para h
3 Método de Euler contra métodos de ordem maior
4 Notas
5 Ver também
Formulação do Método de Euler |
Suponha que queremos aproximar a solução de um problema de valor inicial:
- y′(t)=f(t,y(t)),y(t0)=y0.{displaystyle y'(t)=f(t,y(t)),qquad qquad y(t_{0})=y_{0}.}
Escolhendo um valor para h{displaystyle h}
yn+1=yn+hf(tn,yn).{displaystyle y_{n+1}=y_{n}+hf(t_{n},y_{n}).}Com isso, para um valor menor de h{displaystyle h}
O valor de yn{displaystyle y_{n}}
Enquanto o Método de Euler integra uma EDO de primeira ordem, qualquer EDO de ordem N pode ser representada como uma equação de primeira ordem: tendo a equação
y(N)(t)=f(t,y(t),y′(t),…,y(N−1)(t)){displaystyle y^{(N)}(t)=f(t,y(t),y'(t),ldots ,y^{(N-1)}(t))},
temos a introdução de variáveis auxiliares z1(t)=y(t),z2(t)=y′(t),…,zN(t)=y(N−1)(t){displaystyle z_{1}(t)=y(t),z_{2}(t)=y'(t),ldots ,z_{N}(t)=y^{(N-1)}(t)}
z′(t)=(z1′(t)⋮zN−1′(t)zN′(t))=(y′(t)⋮y(N−1)(t)y(N)(t))=(z2(t)⋮zN(t)f(t,z1(t),…,zN(t))){displaystyle mathbf {z} '(t)={begin{pmatrix}z_{1}'(t)\vdots \z_{N-1}'(t)\z_{N}'(t)end{pmatrix}}={begin{pmatrix}y'(t)\vdots \y^{(N-1)}(t)\y^{(N)}(t)end{pmatrix}}={begin{pmatrix}z_{2}(t)\vdots \z_{N}(t)\f(t,z_{1}(t),ldots ,z_{N}(t))end{pmatrix}}}
Este é um sistema de primeira ordem na variável z(t){displaystyle mathbf {z} (t)}
Exemplo |
Dado o problema de valor inicial
- y′=y,y(0)=1,{displaystyle y'=y,quad y(0)=1,}
vamos usar o método de Euler para aproximar y(4){displaystyle y(4)}
Usando um passo igual a 1 (h = 1) |
Ilustração da integração numérica para o exemplo y′=y,y(0)=1.{displaystyle y'=y,y(0)=1.}
[5] A curva em Azul é o método de Euler com h = 1.0.; em Verde, o ponto médio e em Vermelho, o valor exato da solução, y=et.{displaystyle y=e^{t}.}
O método de Euler é
- yn+1=yn+hf(tn,yn).{displaystyle y_{n+1}=y_{n}+hf(t_{n},y_{n}).qquad qquad }
Primeiramente devemos aplicar o ponto f(t0,y0){displaystyle f(t_{0},y_{0})}
- f(t0,y0)=f(0,1)=1.{displaystyle f(t_{0},y_{0})=f(0,1)=1.qquad qquad }
Através do passo acima, vemos que a declividade da linha é tangente à solução da curva no ponto (0,1){displaystyle (0,1)}
O próximo passo é multiplicar o valor acima pelo tamanho do passo h{displaystyle h}
- h⋅f(y0)=1⋅1=1.{displaystyle hcdot f(y_{0})=1cdot 1=1.qquad qquad }
Como o tamanho do passo é a variação em t{displaystyle t}
- y0+hf(y0)=y1=1+1⋅1=2.{displaystyle y_{0}+hf(y_{0})=y_{1}=1+1cdot 1=2.qquad qquad }
Os passos acima devem ser repetidos para assim encontrarmos y2{displaystyle y_{2}}
- y2=y1+hf(y1)=2+1⋅2=4,y3=y2+hf(y2)=4+1⋅4=8,y4=y3+hf(y3)=8+1⋅8=16.{displaystyle {begin{aligned}y_{2}&=y_{1}+hf(y_{1})=2+1cdot 2=4,\y_{3}&=y_{2}+hf(y_{2})=4+1cdot 4=8,\y_{4}&=y_{3}+hf(y_{3})=8+1cdot 8=16.end{aligned}}}
Como isso se torna um processo repetitivo, uma boa forma de organizar cada iteração em forma de tabela, evitando a possibilidade de erros.
n{displaystyle n}
yn{displaystyle y_{n}}
tn{displaystyle t_{n}}
f(tn,yn){displaystyle f(t_{n},y_{n})}
h{displaystyle h}
Δy{displaystyle Delta y}
yn+1{displaystyle y_{n+1}}
0
1
0
1
1
1
2
1
2
1
2
1
2
4
2
4
2
4
1
4
8
3
8
3
8
1
8
16
A conclusão desse método é de que y4=16{displaystyle y_{4}=16}
Usando outros tamanhos para h |
A mesma ilustração para h = 0.25.
Como mostrado no início, o método possui sua aproximação aprimorada quando tomamos valores cada vez menores para h{displaystyle h}
Tamanho de h{displaystyle h}
Resultado do Método de Euler
Erro Absoluto
1
16
38,598
0,25
35,53
19,07
0,1
45,26
9,34
0,05
49,56
5,04
0,025
51,98
2,62
0,0125
53,26
1,34
O erro absoluto é a diferença entre o valor obtido por Euler e o valor exato da solução para t=4{displaystyle t=4}
Em outros métodos ilustrados, como o Método dos Pontos Médios neste caso mostraram-se mais razoáveis, pois este possui uma precisão proporcional quadrática do tamanho do passo. Por essa razão, tem-se o Método de Euler como um método de primeira ordem, enquanto o Método dos Pontos Médios é dito como de segunda ordem.
Podemos extrapolar a tabela acima se precisamos de uma melhor precisão através da escolha de valores como h=0,00001{displaystyle h=0,00001}
Método de Euler contra métodos de ordem maior |
A ordem de um método mede o quanto rapidamente este converge para a solução analítica quando se diminui os passos na integração numérica [7]. Infelizmente devido a limitações computacionais, erros de arredondamento crescem quando se diminui o tamanho dos passos, ocorrendo até mesmo divergência ou mesmo valores errados. Uma forma de resolver este problema é aumentar a ordem do método numérico. Por exemplo, métodos de ordem maiores incluem método de Runge-Kutta e o método de Euler melhorado.
Notas |
↑ «Faça exemplos com O Monitor». omonitor.io. Consultado em 23 de março de 2016
↑ Butcher 2003, p. 45; Hairer, Nørsett & Wanner 1993, p. 36
↑ Butcher 2003, p. 3; Hairer, Nørsett & Wanner 1993, p. 2
↑ Veja Também Atkinson 1989, p. 344
↑ «Confira este exemplo e faça outros com O Monitor». omonitor.io. Consultado em 23 de março de 2016
↑ Hairer, Nørsett & Wanner 1993, p. 40
↑ Devries, Paul L. ; Hasbun, Javier E. A first course in computational physics. Second edition. Jones and Bartlett Publishers: 2011.
Ver também |
- Para métodos numéricos para cálculo de integrais definidas, veja integração numérica.
