Máquina de estados finita

Multi tool use
Uma máquina de estados finita (FSM - do inglês Finite State Machine) ou autômato finito é um modelo matemático usado para representar programas de computadores ou circuitos lógicos. O conceito é concebido como uma máquina abstrata que deve estar em um de um número finito de estados. A máquina está em apenas um estado por vez, este estado é chamado de estado atual. Um estado armazena informações sobre o passado, isto é, ele reflete as mudanças desde a entrada num estado, no início do sistema, até o momento presente. Uma transição indica uma mudança de estado e é descrita por uma condição que precisa ser realizada para que a transição ocorra. Uma ação é a descrição de uma atividade que deve ser realizada num determinado momento.
Máquinas de estado finitas podem modelar um grande número de problemas, entre os quais a automação de design eletrônico, projeto de protocolo de comunicação, análise e outras aplicações de engenharia. Na biologia e na pesquisa da inteligência artificial, máquinas de estado ou hierarquias de máquinas de estado são, por vezes, utilizadas para descrever sistemas neurológicos e em linguística para descrever as gramáticas das linguagens naturais.
Índice
1 Conceitos e Vocabulário
2 Representação
2.1 Diagrama de estados
2.2 Máquinas de estados UML
2.3 Máquinas de estados SDL
2.4 Outros diagramas de estado
3 Uso
4 Classificação
4.1 Aceitadores e reconhecedores
4.1.1 Estado Inicial
4.1.2 Estados de aceitação (ou Estados Finais)
4.2 Transdutores
4.3 Determinismo
5 Semânticas Alternativas
6 Lógica da FSM
7 Modelo matemático
8 Implementação
8.1 Aplicações de Hardware
8.2 Aplicações de Software
9 Referências
10 Ligações externas
Conceitos e Vocabulário |
Um estado descreve um nó de comportamento do sistema em que está à espera de uma condição para executar uma transição. Normalmente, um estado é introduzido quando o sistema não reage da mesma forma para uma mesma condição. No exemplo de um sistema de rádio de carro, quando se está ouvindo uma estação de rádio, o estímulo "próximo" significa ir para a próxima estação. Mas quando o sistema está no estado de CD, o estímulo "próximo" significa ir para a próxima faixa. O mesmo estímulo desencadeia ações diferentes, dependendo do estado atual. Em algumas representações de máquinas de estado finitas, também é possível associar ações a um estado:
- Ação de entrada: o que é realizado ao entrar no estado,
- Ação de saída: o que é executado ao sair do estado.
A transição é um conjunto de ações a serem executadas quando uma condição for cumprida ou quando um evento é recebido.
Máquinas de estado são utilizadas para descrever circuitos sequenciais. Diferentemente de um contador que em geral conta eventos, uma máquina de estado costuma ser usada para controlar o evento.
A máquina está em apenas um estado por vez, este estado é chamado de estado atual. Um estado armazena informações sobre o passado, isto é, ele reflete as mudanças desde a entrada num estado, no início do sistema, até o momento presente. Uma transição indica uma mudança de estado e é descrita por uma condição que precisa ser realizada para que a transição ocorra. Uma ação é a descrição de uma atividade que deve ser realizada num determinado momento.
Representação |

Fig. 1 Exemplo de máquina de estados SDL

Fig. 2 Exemplo de uma máquina de estados finita simples
Diagrama de estados |
Máquinas de estados finitas podem ser representadas por meio de um diagrama de estados (ou diagrama de transição de estados). Diversas tabelas de transição de estados são usadas, a mais famosa é a mostrada abaixo. A combinação do estado atual (ex: B) com uma condição (ex: Y) determina o próximo estado (ex: C).
Através do uso das tabelas podemos representar uma máquina finita de estados que contenha informações completas sobre as ações.
| Estado Atual → Condição ↓ |
Estado A | Estado B | Estado C |
|---|---|---|---|
| Condição X |
... | ... | ... |
| Condição Y |
... | Estado C | ... |
| Condição Z |
... | ... | ... |
Máquinas de estados UML |
A UML tem uma notação para descrever máquinas de estado. Máquinas de estado UML superam as limitações das FSMs tradicionais, mantendo os seus principais benefícios. Máquinas de estados UML introduzem os novos conceitos de estados aninhados hierarquicamente e regiões ortogonais, enquanto estende a noção de ações. Máquinas de estado UML têm as características de ambas as máquinas de Mealy e Moore. Elas suportam ações que dependem tanto do estado do sistema quanto da condição, como em máquinas de Mealy, assim como ações de entrada e saída que estão associadas com os estados em vez de transições, como em máquinas de Moore.
Máquinas de estados SDL |
A SDL é um padrão da União Internacional de Telecomunicações e é uma das melhores linguagens para descrever máquinas de estado, pois inclui símbolos gráficos para descrever as ações na transição:
- enviar um evento
- receber um evento
- iniciar um temporizador
- cancelar um temporizador
- iniciar uma nova máquina de estado simultânea
- decisão
SDL incorpora tipos básicos de dados chamado Abstract Data Types, uma linguagem de ação, e uma semântica de execução, a fim de tornar a máquina de estados finita executável. Um exemplo é visto na figura 1.
Outros diagramas de estado |
Existem várias outras maneiras de se representar uma FSM, assim como mostrado na figura 2.
Um exemplo é o HDL:
Em HDL (Hardware Description Language) ou LDH(Linguagem de Descrição de Hardware) é possível criar máquinas de estado simples e de descrição intuitiva. É feito o uso de estados nomeados para os quais não há valores binários definidos.
Em VHDL existem as palavras-chave como TYPE por exemplo, que define o tipo enumerado em VHDL. O projetista lista em nomes simbólicos (diferentes das palavras-chave) todos os possíveis valores que um sinal, variável ou porta que é declarado como sendo deste tipo pode assumir. O valor binário é determinado pelo compilador, deixando o trabalho do projetista mais simples.
Uso |
Além de seu uso na modelagem de sistemas reativos aqui apresentados, máquinas de estados finitas são significativos em diversas áreas, incluindo engenharia elétrica, linguística, ciência da computação, filosofia, biologia, matemática e lógica. Máquinas de estados finitas são uma classe de autômatos estudada na teoria dos autômatos e teoria da computação. Em ciência da computação, máquinas de estados finitas são amplamente utilizados na modelagem do comportamento do aplicativo, design de sistemas digitais de hardware, engenharia de software, compiladores, protocolos de rede, e o estudo da computação e linguagens.
Classificação |
Existem dois grupos: Aceitadores/Reconhecedores e Transdutores.
Aceitadores e reconhecedores |
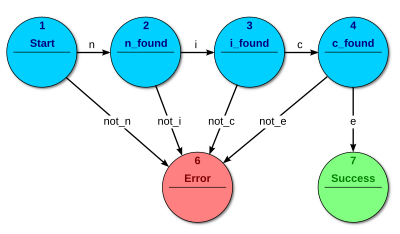
Fig. 3 FSM aceitador: analisando a palavra "nice"
Aceitadores e reconhecedores produzem uma saída binária, dizendo sim ou não para responder se a entrada é aceita pela máquina ou não. Todos os estados do FSM estão a dizer se quer aceitar ou não quer aceitar. No momento em que todas as entradas são processadas, se o estado atual é um estado de aceitação, a entrada é aceita, caso contrário é rejeitada. Como regra a entrada são símbolos (caracteres); ações não são usadas. O exemplo da figura 3 mostra uma máquina de estados finita que aceita a palavra "nice". Neste FSM o único estado de aceitação é o número 7.
A máquina também pode ser descrita como a definição de uma linguagem, que conteria todas as palavras aceitas pela máquina e nenhuma das que são rejeitadas; dizemos então que a linguagem é aceita pela máquina. Por definição, linguagens aceitas por FSMs são as linguagens regulares, isto é, uma linguagem é regular se existe alguma FSM que a aceita.
Estado Inicial |
O estado inicial é geralmente mostrado desenhando uma seta "apontando para ele a partir de qualquer lugar" (Sipser (2006) p. 34).
Estados de aceitação (ou Estados Finais) |

Fig. 4: Representação de uma FSM. Este exemplo mostra uma FSM que determina se um número binário tem um número par ou ímpar de 0's, onde S1 é um estado de aceitação.
Estados de aceitação são aqueles em que a máquina relata que a seqüência de entrada, como processadas até agora, é membro da linguagem que ela aceita. É geralmente representado por um círculo duplo.
Um exemplo de um estado de aceitação aparece na figura 4: um autômato finito determinístico (AFD) que detecta se a seqüência de entrada binária contém um número par de 0's.
S1 (que também é o estado inicial) indica o estado no qual um número par de 0's foi dado na entrada. S1 é, portanto, um estado de aceitação. Esta máquina vai terminar em um estado de aceitação se a seqüência binária contém um número par de 0's (incluindo qualquer seqüência binária que não contenham 0's). Exemplos de cadeias aceitas por este AFD são: epsilon (a cadeia vazia), 1, 11, 11 ..., 00, 010, 1010, 10110, etc.
Transdutores |
Transdutores geram uma saída baseada em uma entrada e/ou um estado utilizando ações. Eles são utilizados para aplicações de controle.
A saída produzida por um contador ou uma máquina de estado pode vir diretamente das saídas do flip-flop, ou alguns circuitos lógicos. As duas variações são chamadas de modelo Mealy de circuitos sequencial e modelo Moore.
No modelo Mealy, os sinais de saída também são controlados por sinais de entrada adicionais, enquanto o modelo Moore não possui nenhum controle externos para os sinais de saída gerados.A saída do modelo Moore é função apenas do estado atual do flip-flop.
As saídas de um circuito de tipo Moore serão completamente síncronas em relação ao clock do circuito, enquanto saídas produzidas por um circuito de tipo Mealy podem mudar assincronamente.
- Máquina de Moore
- A FSM utiliza apenas ações de entrada, i.e. a saída depende somente do estado. A vantagem do modelo de Moore é a simplificação do comportamento. Consideremos por exemplo uma FSM de Moore de uma porta de elevador com 4 estados "Aberta", "Fechada", "Abrindo", "Fechando". A máquina de estados reconhece dois comandos: "comando_abrir" e "comando_fechar" que disparam a alteração de estado. A ação de entrada (E:) no estado "Abrindo" liga o motor que abre a porta, a ação de entrada no estado "Fechando" liga o motor na outra direção, fechando a porta. Os estados "Aberta" e "Fechada" não desempenham nenhuma ação. Eles sinalizam para o mundo externo (e.g. para outras máquinas de estado) a situação: "porta está aberta" ou "porta está fechada".

Fig. 5 FSM transdutor: exemplo do modelo de Mealy
- Máquina de Mealy
- A FSM utiliza apenas input actions, i.e. a saída depende da entrada e do estado. O uso de uma FSM de Mealy normalmente leva a uma redução no número de estados. Por exemplo uma FSM de Mealy implementando o mesmo comportamento visto no exemplo de Moore (o comportamento depende no modelo de execução implementado na FSM e irá funcionar e.g. para uma FSM virtual mas não para uma FSM de eventos dirigidos). Existem duas input actions(I:): “inicie o motor para fechar a porta se o comando_fechar (sensor_closed na figura 5) chegar” e “inicie o motor na direção oposta para abrir a porta se o comando_abrir (sensor_opened na figura 5) chegar”.
Na prática modelos mistos são muito utilizados.
Mais detalhes sobre as diferenças e usos dos modelos de Moore e Mealy, incluindo um exemplo executável, podem ser encontrados na nota técnica externa "Modelo de Moore ou Mealy?"(documento em inglês)
Determinismo |
Uma distinção adicional está entre autômato determinístico (AFD) e não-determinístico (AFN). No autômato determinístico, para cada estado há exatamente uma transição para cada entrada possível. No autômato não determinístico, pode haver nenhuma, uma ou mais de uma transição de um determinado estado para uma entrada possível.
A FSM com apenas um estado é chamada de FSM combinatória e utiliza apenas input actions. Este conceito é útil quando um número de FSM devem trabalhar juntas, e onde é conveniente considerar uma parte puramente combinatória como uma forma de FSM para se adequar às ferramentas de projeto.
Semânticas Alternativas |
Há outros conjuntos de semântica disponível para representar máquinas de estado. Por exemplo, existem ferramentas para modelagem e lógica para projetar controladores incorporados.[1] Eles combinam máquinas de estado hierárquico, gráficos de fluxo e tabelas de verdade para uma linguagem, resultando em um diferente formalismo e conjunto de semântica.[2] A Figura 6 ilustra esta mistura de máquinas de estado e gráficos de fluxo com um conjunto de estados para representar o estado de um cronômetro e um gráfico de fluxo para controlar os tiques do relógio. Estes gráficos, como máquinas de estado originais de Harel,[3] apoiam os estados hierarquicamente aninhados, regiões ortogonais, ações do estado, e as ações de transição.[4]
Lógica da FSM |

Fig. 6 Lógica da FSM (Mealy)
O próximo estado e a saída de uma FSM são uma função da entrada e do atual estado. A lógica da FSM é mostrada na figura 6.
Modelo matemático |
Dependendo do tipo pode haver várias definições.
Uma máquina de estados finita tipo aceitador é uma quíntupla <Σ, S, s0, δ, F>, onde:
Σ é o alfabeto de entrada (um conjunto finito, não vazio, de símbolos);
S é um conjunto finito, não vazio, de estados;
s0 é o estado inicial, um elemento de S;
δ é a função de transição de estados: δ: S x Σ → S (em um AFN, seria δ: S x Σ → P(S), isto é, δiria retornar um conjunto de estados);
F é o conjunto de estados finais, um (possivelmente vazio) subconjunto de S.
Para ambos os FSMs determinísticas e não-deterministica, é convencional para permitir δ ser uma função parcial, ou seja, δ(q, x) não tem que ser definida para cada combinação de q ∈{displaystyle in }

Uma máquina de estados finita é uma máquina de Turing restrita em que a cabeça só pode "ler" as operações, e sempre se move da esquerda para a direita.[5]
Uma máquina de estados finita tipo transdutor é uma sêxtupla <Σ, Γ, S, s0, δ, ω>, onde:
Σ é o alfabeto de entrada (um conjunto finito, não vazio, de símbolos);
Γ é o alfabeto de saída (um conjunto finito, não vazio, de símbolos);
S é um conjunto finito, não vazio, de estados;
s0 é o estado inicial, um elemento de S;
δ é a função de transição de estados: δ: S x Σ → S (em um AFN, seria δ: S x Σ → P(S), isto é, δiria retornar um conjunto de estados);
ω é a função de saída.
Se a função de saída é uma função do estado e do alfabeto de entrada (ω: S x Σ → Γ )essa definição corresponde ao modelo de Mealy. Se a função de saída depende somente do estado (ω: S → Γ ) essa definição corresponde ao modelo de Moore.
Se desconsiderarmos o símbolo primeira saída de uma máquina de Moore, ω(s0), então ela pode ser facilmente convertida em uma máquina de Mealy de saída equivalente definindo a função de saída de cada transição da de Mealy (isto é, rotulando cada extremidade) com o símbolo de saída dado ao estado de destino da de Moore. A transformação inversa é menos simples, porque um estado da máquina de Mealy pode ter rótulos de saída diferentes em suas transições de entrada (extremidades). Cada estado tem de ser dividido em vários estados da máquina de Moore, uma para cada símbolo de saída incidente.[6]
Teoria de autômatos: linguagem formal e gramática formal | |||
|---|---|---|---|
Hierarquia Chomsky |
Gramática |
Linguagem |
Reconhecedor |
| Tipo-0 |
Irrestrita |
Recursivamente enumerável |
Máquina de Turing |
| -- |
-- |
Recursiva |
Máquina de Turing que sempre para |
| Tipo-1 |
Sensível ao contexto |
Sensível ao contexto |
Autômato linearmente limitado |
| Tipo-2 |
Livre de contexto |
Livre de contexto |
Autômato com pilha |
| Tipo-3 |
Regular |
Regular |
Autômato finito |
Implementação |
Aplicações de Hardware |

Fig. 7 O diagrama de circuito para um contador TTL de 4bits, um tipo de máquina de estados
Em um circuito digital, uma FSM pode ser construída utilizando um dispositivo lógico programável. Um controlador lógico programável, portas lógicas e flip-flops ou relays. Mais especificamente, a implementação de hardware requer um registrador para armazenar o estado das variáveis, um bloco de lógica combinacional que determina o estado de transição e um segundo bloco de lógica combinacional que determina a saída da FSM.
O mais famoso é o controlador de Richards
Máquinas de Mealy e de Moore produzem lógica com saída assíncrona, porque há um atraso de propagação entre o flip-flop e saída. Isso causa frequências mais lentas operando na FSM. Uma máquina de Mealy ou de de Moore pode ser convertida para uma FSM tal qual a saída é diretamente de um flip-flop, o que faz a FSM funcionar em frequências mais altas. Este tipo de FSM é chamado às vezes FSM de Medvedev.[7] Um contador é a forma mais simples desse tipo de FSM.
Aplicações de Software |
Os seguintes conceitos são comumente usados para construir aplicações de software com máquinas de estados finitas:
- Programação baseada em autômatos
- FSM orientada a eventos
- FSM Virtual (VFSM)
Referências |
↑ Tiwari, A. (2002). Formal Semantics and Analysis Methods for Simulink Stateflow Models.
↑ Hamon, G. (2005). A Denotational Semantics for Stateflow. International Conference on Embedded Software (pp. 164–172). Jersey City, NJ: ACM.
↑ Harel, D. (1987). A Visual Formalism for Complex Systems. Science of Computer Programming , 231–274.
↑ «Alur, R., Kanade, A., Ramesh, S., & Shashidhar, K. C. (2008). Symbolic analysis for improving simulation coverage of Simulink/Stateflow models. Internation Conference on Embedded Software (pp. 89–98). Atlanta, GA: ACM.» (PDF). Consultado em 9 de dezembro de 2011. Arquivado do original (PDF) em 15 de julho de 2011
↑ Black, Paul E (12 de maio de 2008). «Finite State Machine». U.S. National Institute of Standards and Technology. Dictionary of Algorithms and Data Structures
↑ James Andrew Anderson; Thomas J. Head (2006). Automata theory with modern applications. [S.l.]: Cambridge University Press. pp. 105–108. ISBN 9780521848879
↑ «FSM: Medvedev». Consultado em 9 de dezembro de 2011. Arquivado do original em 19 de julho de 2011
- Timothy Kam, Synthesis of Finite State Machines: Functional Optimization. Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9842-4
- Tiziano Villa, Synthesis of Finite State Machines: Logic Optimization. Kluwer Academic Publishers, Boston 1997, ISBN 0-7923-9892-0
- Carroll, J., Long, D. , Theory of Finite Automata with an Introduction to Formal Languages. Prentice Hall. Englewood Cliffs, 1989.
- Hopcroft, J.E., Ullman, J.D., Introduction to Automata Theory, Languages and Computation. Addison -Wesley, 1979.
- Kohavi, Z., Switching and Finite Automata Theory. McGraw-Hill, 1978.
- Gill, A., Introduction to the Theory of Finite-state Machines. McGraw-Hill, 1962.
- Cassandras, C., Lafortune, S., "Introduction to Discrete Event Systems". Kluwer, 1999, ISBN 0-7923-8609-4
- Tocci, Ronald J., "Sistemas digitais:Princípios e aplicações.", 10ª edição, 2007
Ligações externas |
Description from the Free On-Line Dictionary of Computing[ligação inativa]
- NIST Dictionary of Algorithms and Data Structures entry
- Hierarchical State Machines
8n347S04hchwdeHVhNq8d
